I spent the weekend trying to implement SIFT based on Lowe’s paper “Distinctive Image Features from Scale-Invariant Keypoints.” Needless to say it was a fun weekend. The main focus was on the first two steps of the algorithm: “Detection of scale-space extrema” and “Accurate keypoint localization.”
The implementation of the first two steps is not working properly yet. There seems to be a bug in the function that builds the scale-space pyramids. Specifically sigma values used to create the five Gaussian images of each octave appear incorrect. When the initial sigma was set to 1.0, no keypoints were found on any octave, and when the initial sigma was dropped to 0.7, approximately 4,500 keypoints were found in the test image. The test program used three octaves and most of the keypoints were found in the first two octaves. The last octave found under 20 keypoints. Compare this to Lowe’s results on a 233 x 189 image, where 832 initial keypoints were found and 536 keypoints remained after “thresholding on ratio of principal curvatures.” The test image used in this implementation is 583 x 395, about double the size. Nine times the number of keypoints found seems wrong. In addition, the keypoints are scattered all over the image and don’t appear to correspond to actual corners or edges.
Fig. 1 - Test image

Additional implementation notes:
Use double instead of uchar
64 bit floating point (double) values between 0.0 and 1.0 are used instead if unsigned chars (uchar) values between 0 and 255. This increases the precision and appears to create more keypoints.
Octaves
One octave is the set of images at a particular level of the pyramid. For example octave 1 would consist of five Gaussian blurred images with resolution 1166 x 790, three Difference of Gaussians (DoG) images at the same resolution, and two images that contain keypoints. Lowe’s paper has a good diagram on page 6.
Maxima and minima of DoG images
The maxima and minima of the DoG images is calculated by comparing the 8 neighboring pixels on current image and the 18 pixels from images above and below. This is 36 comparisons for each pixel of the image. Luckily not all comparisons are needed since the algorithm is searching for the smallest (minima) or largest (maxima) pixel. Lowe’s paper has a good diagram on page 7.
Calculating DoGs
The equation to calculate the DoG requires two Gaussian images. The first image has a sigma that is a factor of k larger or smaller than the second image. Here D represents the DoG image. G appears to represent the Gaussian kernels and I represents the image.
D(x, y, σ) = (G(x, y, kσ) − G(x, y, σ)) ∗ I(x, y)
Since the SIFT algorithm already calculates the images Gaussian blur of the images separately, we can factor I into each of the Gaussian kernels separately. In the modified equation L represents G(x, y, kσ) ∗ I(x, y) and G(x, y, σ) ∗ I(x, y)
D(x, y, σ) = L(x, y, kσ) − L(x, y, σ)
Another thing to note is that the DoG can have negative values since they are not really images. To visual the DoG values better, 0.5 can be added to each value.
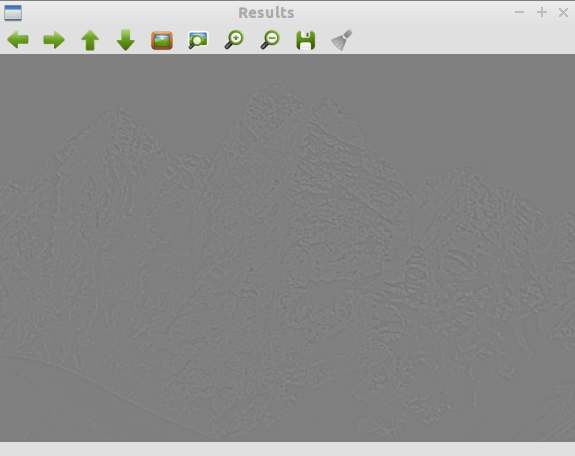
Fig. 2 - DoG calculation with 0.5 added to value in matrix to improve visibility for visualization
Calculating sigma and k for Gaussian images
This is where my implementation falls apart, specifically on the matter of what value of k to use and what value of sigma to use for each successive Gaussian image.
On page 7 of Lowe’s paper, k = 2^{1/s}, where s appears to be the number of images desired for calculating the minima and maxima. In this case, s = 2 and k = \sqrt{2} = 2^{1/2}. This is just guess a though, since the paper specifies that there will be s + 3 blurred images.
The part is clear, but it remains unclear how to calculate successive sigma values. For instance is it as simple as multiplying the previous sigma with k? Thishis SIFT article from AI Shack seems to describe this approach. Here are similar numbers reproduced using a starting sigma of 1.0 and k of square of 2. Each new sigma is calculated by multiplying k with the previous sigma. The next octave starts with the sigma of the third image. Lowe’s paper says to subsample the third Gaussian image of the previous octave. This saves calculations.
| Octave 1 | 1.0 | 1.41 | 2 | 2.83 | 4 |
| Octave 2 | 1.41 | 2 | 2.83 | 4 | 5.66 |
Looking at the table, the sigma value seems to double at every other image in the octave. Is this correct? Or should the sigma only double at the last image?
One possible error in my implementation could be this line:
gaussian_blur(gauss[i - 1], gauss[i], scale[i % num_scales]);
Here the Gaussian blur is applied to the previous image and not the first image. It seems like the first image makes more sense since the previous image would already have a Gaussian blur applied. Wouldn’t this increase the sigma factor?
Of the four SIFT implementations that I studied, there were 3 different approaches to calculate the Gaussian pyramid.
- Source code for Open CV SIFT implementation
- Open CV SIFT is based off of this implementation
- Yet another Open CV SIFT implementation
- SIFT implementation using VXL
Fig. 3 - Gaussian blur on octave 2 image 1
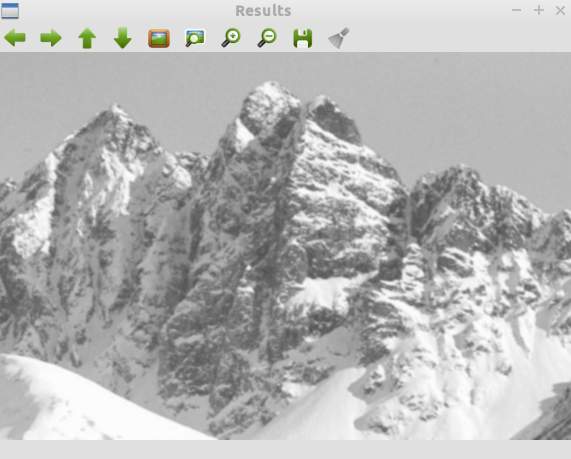
Fig. 4 - Gaussian blur on octave 2 image 4
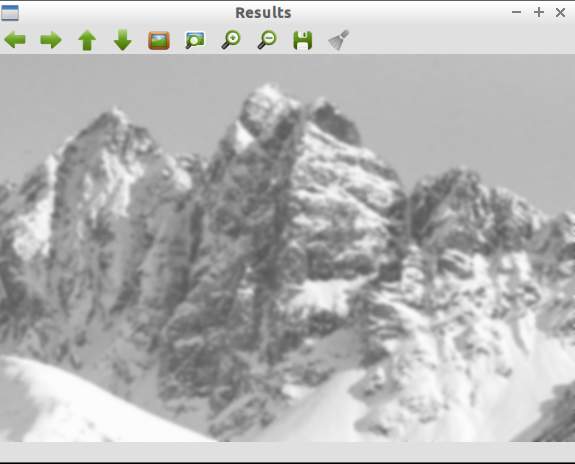
Eliminating edge responses
This part was difficult to understand, mainly because of the Linear Algebra and Calculus in three dimensions that is required to understand how edge responses are eliminated. Edge responses are minima and maxima that correspond to edges in the image. These points do not handle change in scale and noise as well as corners apparently.
To eliminate edge responses, Lowe uses a Hessian matrix to compute something called the principal curvature.
| Dxx | Dxy |
| Dxy | Dyy |
How are Dxx, Dyy, and Dxy calculated or what do they represent? Apparently these are derivatives that can be estimated by subtracting neighboring pixels. Once we have these values, it seems that we can just plug in the values to solve these two equations, where alpha and beta are eigenvalues. These values can be ignored since we will only be using Dxx, Dyy, and Dxy to perform the calculations.
Tr(H) = Dxx + Dyy = α + β and
Det(H) = Dxx * Dyy − (Dxy)^2 = αβ.
After that we divide Tr(H) squared by the Det(H) to find the ration. Then we keep the point if the ratio is less than some value r. Lowe uses 10 in his paper. These equations are found on page 12.
Once again it was interesting to see how different the implementations were.
Fig. 5 - Keypoints after edge responses eliminated in octave 2
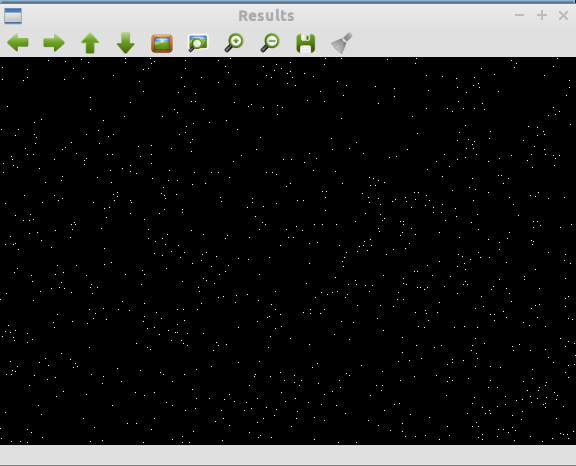
Fig. 4 - Keypoints after edge responses eliminated in octave 3
Source (WIP)
#include <iostream>
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <unistd.h>
#include <opencv2/imgproc/imgproc.hpp>
#include <opencv2/highgui/highgui.hpp>
// User Settings
#define WINDOW_NAME "Results"
#define IMAGE "chugach-mtns.jpg"
#define SHOW_GAUSSIANS true
#define SHOW_DOGS true
#define SHOW_EXTREMA true
// Grayscale Settings
#define R_WEIGHT 0.21
#define G_WEIGHT 0.71
#define B_WEIGHT 0.07
// Gaussian Blur Settings
#define KERNEL_SIZE 3
// Difference of Gaussians Settings
#define NUM_OCTAVES 3
#define NUM_SCALES 5
#define PRE_BLUR_SIGMA 0.5
#define INITIAL_SIGMA 0.7
// Extrema Detection Settings
#define CONTRAST_THRESHOLD 0.03
// Constant Constants
#define MAX_8BIT 255
using namespace cv;
using namespace std;
void grayscale(Mat src, Mat &gray)
{
gray = Mat::zeros(src.rows, src.cols, CV_64F);
Vec3b rgb;
for (int i = 0; i < src.rows; ++i) {
for (int j = 0; j < src.cols; ++j) {
rgb = src.at<Vec3b>(i, j);
gray.at<double>(i, j) = R_WEIGHT * rgb[0] + G_WEIGHT * rgb[1] + B_WEIGHT * rgb[2];
}
}
}
void normalize(Mat src, Mat &norm)
{
norm = Mat::zeros(src.rows, src.cols, CV_64F);
for (int i = 0; i < src.rows; ++i) {
for (int j = 0; j < src.cols; ++j) {
norm.at<double>(i, j) = src.at<double>(i, j) / MAX_8BIT;
}
}
}
void scale_down_2x(Mat src, Mat &scaled)
{
scaled = Mat::zeros(src.rows / 2, src.cols / 2, CV_64F);
int i;
int j;
for (i = 0; i < scaled.rows; ++i) {
for (j = 0; j < scaled.cols; ++j) {
scaled.at<double>(i, j) = src.at<double>(i * 2, j * 2);
}
}
}
void scale_up_2x(Mat src, Mat &scaled)
{
scaled = Mat::zeros(src.rows * 2, src.cols * 2, CV_64F);
double p0;
double p1;
int i;
int j;
for (i = 0; i < src.rows; ++i) {
for (j = 0; j < src.cols; ++j) {
scaled.at<double>(i * 2, j * 2) = src.at<double>(i, j);
if (i + 1 == src.rows) {
scaled.at<double>(i * 2 + 1, j * 2) = src.at<double>(i, j);
} else {
p0 = src.at<double>(i, j);
p1 = src.at<double>(i + 1, j);
scaled.at<double>(i * 2 + 1, j * 2) = p0 + (p1 - p0) * 0.5;
}
if (j + 1 == src.cols) {
scaled.at<double>(i * 2, j * 2 + 1) = src.at<double>(i, j);
} else {
p0 = src.at<double>(i, j);
p1 = src.at<double>(i, j + 1);
scaled.at<double>(i * 2, j * 2 + 1) = p0 + (p1 - p0) * 0.5;
}
if (i + 1 == src.rows || j + 1 == src.cols) {
scaled.at<double>(i * 2 + 1, j * 2 + 1) = src.at<double>(i, j);
} else {
p0 = src.at<double>(i, j);
p1 = src.at<double>(i + 1, j + 1);
scaled.at<double>(i * 2 + 1, j * 2 + 1) = p0 + (p1 - p0) * 0.5;
}
}
}
}
void gaussian_blur(Mat src, Mat &blur, double sigma)
{
blur = src.clone();
double xdist[KERNEL_SIZE][KERNEL_SIZE] =
{
{1, 1, 1},
{0, 0, 0},
{1, 1, 1}
};
double ydist[KERNEL_SIZE][KERNEL_SIZE] =
{
{1, 0, 1},
{1, 0, 1},
{1, 0, 1}
};
double kernel[KERNEL_SIZE][KERNEL_SIZE];
double sum = 0;
double sigFactor = 1.0 / (2.0 * M_PI * sigma * sigma);
int x;
int y;
int i;
int j;
double p0;
double p1;
double p2;
double p3;
double p4;
double p5;
double p6;
double p7;
double p8;
for (x = 0; x < KERNEL_SIZE; ++x) {
for (y = 0; y < KERNEL_SIZE; ++y) {
kernel[x][y] = sigFactor * exp(-((xdist[x][y] + ydist[x][y]) / (2.0 * sigma * sigma)));
sum += kernel[x][y];
}
}
for (x = 0; x < KERNEL_SIZE; ++x) {
for (y = 0; y < KERNEL_SIZE; ++y) {
kernel[x][y] = kernel[x][y] / sum;
}
}
for (i = 1; i < blur.rows - 1; ++i) {
for (j = 1; j < blur.cols - 1; ++j) {
p0 = src.at<double>(i - 1, j - 1);
p1 = src.at<double>(i - 1, j);
p2 = src.at<double>(i - 1, j + 1);
p3 = src.at<double>(i, j - 1);
p4 = src.at<double>(i, j);
p5 = src.at<double>(i, j + 1);
p6 = src.at<double>(i + 1, j - 1);
p7 = src.at<double>(i + 1, j);
p8 = src.at<double>(i + 1, j + 1);
blur.at<double>(i, j) =
p0 * kernel[0][0] + p1 * kernel[0][1] + p2 * kernel[0][2] +
p3 * kernel[1][0] + p4 * kernel[1][1] + p5 * kernel[1][2] +
p6 * kernel[2][0] + p7 * kernel[2][1] + p8 * kernel[2][2];
}
}
}
void diff_of_gaussians(Mat gauss1, Mat gauss2, Mat &dog)
{
dog = Mat::zeros(gauss1.rows, gauss1.cols, CV_64F);
int diff = 0;
int i;
int j;
for (i = 0; i < dog.rows; ++i) {
for (j = 0; j < dog.cols; ++j) {
dog.at<double>(i, j) = gauss2.at<double>(i, j) - gauss1.at<double>(i, j);
}
}
}
void scale_space_pyramid(Mat src, Mat gauss[], Mat dogs[], double sigma, int num_octaves, int num_scales)
{
int num_images = num_octaves * num_scales;
int dog_count = 0;
double scale[num_scales];
double sig_prev = 0;
double sig_total = 0;
int i;
double k = pow(2.0, 1.0 / (num_scales - 3));
scale[0] = sigma;
for (i = 1; i < num_scales; ++i) {
sig_prev = pow(k, i - 1) * sigma;
sig_total = sig_prev * k;
scale[i] = sqrt(sig_total * sig_total - sig_prev * sig_prev);
}
gaussian_blur(src, gauss[0], scale[0]);
for (i = 1; i < num_images; ++i) {
if (i % num_scales == 0) {
scale_down_2x(gauss[i - num_scales + (num_scales - 3)], gauss[i]);
} else {
gaussian_blur(gauss[i - 1], gauss[i], scale[i % num_scales]);
diff_of_gaussians(gauss[i - 1], gauss[i], dogs[dog_count++]);
}
}
}
void detect_extrema(Mat dogs[], Mat extremas[], int num_octaves, int num_dogs)
{
int dogs_per_octave = num_dogs / num_octaves;
Mat image_above;
Mat image;
Mat image_below;
int rows;
int cols;
int i;
int h;
int w;
double val;
Mat extrema;
int extrema_count = 0;
int found = 0;
for (i = 0; i < num_dogs; ++i) {
if (i % dogs_per_octave == 0) {
extrema = Mat::zeros(dogs[i].rows, dogs[i].cols, CV_64F);;
} else if ((i + 1) % dogs_per_octave > 0) {
rows = dogs[i].rows - 1;
cols = dogs[i].cols - 1;
image_above = dogs[i + 1];
image = dogs[i];
image_below = dogs[i - 1];
for (h = 1; h < rows; ++h) {
for (w = 1; w < cols; ++w) {
val = image.at<double>(h, w);
if (
(
abs(val) < CONTRAST_THRESHOLD &&
val > image.at<double>(h - 1, w - 1) &&
val > image.at<double>(h - 1, w) &&
val > image.at<double>(h - 1, w + 1) &&
val > image.at<double>(h, w - 1) &&
val > image.at<double>(h, w + 1) &&
val > image.at<double>(h + 1, w - 1) &&
val > image.at<double>(h + 1, w) &&
val > image.at<double>(h + 1, w + 1) &&
val > image_above.at<double>(h - 1, w - 1) &&
val > image_above.at<double>(h - 1, w) &&
val > image_above.at<double>(h - 1, w + 1) &&
val > image_above.at<double>(h, w - 1) &&
val > image_above.at<double>(h, w) &&
val > image_above.at<double>(h, w + 1) &&
val > image_above.at<double>(h + 1, w - 1) &&
val > image_above.at<double>(h + 1, w) &&
val > image_above.at<double>(h + 1, w + 1) &&
val > image_below.at<double>(h - 1, w - 1) &&
val > image_below.at<double>(h - 1, w) &&
val > image_below.at<double>(h - 1, w + 1) &&
val > image_below.at<double>(h, w - 1) &&
val > image_below.at<double>(h, w) &&
val > image_below.at<double>(h, w + 1) &&
val > image_below.at<double>(h + 1, w - 1) &&
val > image_below.at<double>(h + 1, w) &&
val > image_below.at<double>(h + 1, w + 1)
)
||
(
abs(val) < CONTRAST_THRESHOLD &&
val < image.at<double>(h - 1, w - 1) &&
val < image.at<double>(h - 1, w) &&
val < image.at<double>(h - 1, w + 1) &&
val < image.at<double>(h, w - 1) &&
val < image.at<double>(h, w + 1) &&
val < image.at<double>(h + 1, w - 1) &&
val < image.at<double>(h + 1, w) &&
val < image.at<double>(h + 1, w + 1) &&
val < image_above.at<double>(h - 1, w - 1) &&
val < image_above.at<double>(h - 1, w) &&
val < image_above.at<double>(h - 1, w + 1) &&
val < image_above.at<double>(h, w - 1) &&
val < image_above.at<double>(h, w) &&
val < image_above.at<double>(h, w + 1) &&
val < image_above.at<double>(h + 1, w - 1) &&
val < image_above.at<double>(h + 1, w) &&
val < image_above.at<double>(h + 1, w + 1) &&
val < image_below.at<double>(h - 1, w - 1) &&
val < image_below.at<double>(h - 1, w) &&
val < image_below.at<double>(h - 1, w + 1) &&
val < image_below.at<double>(h, w - 1) &&
val < image_below.at<double>(h, w) &&
val < image_below.at<double>(h, w + 1) &&
val < image_below.at<double>(h + 1, w - 1) &&
val < image_below.at<double>(h + 1, w) &&
val < image_below.at<double>(h + 1, w + 1)
)
) {
extrema.at<double>(h, w) = 1.0;
double dxx =
(image.at<double>(h - 1, w) + image.at<double>(h - 1, w)) - 2.0 * val;
double dyy =
(image.at<double>(h, w - 1) + image.at<double>(h, w + 1)) - 2.0 * val;
double dxy =
(image.at<double>(h - 1, w - 1) +
image.at<double>(h + 1, w + 1) -
image.at<double>(h + 1, w - 1) -
image.at<double>(h - 1, w + 1)) / 4.0;
double trH = dxx + dyy;
double detH = dxx * dyy - dxy * dxy;
double R = ((10.0 + 1) * (10.0 + 1)) / 10.0;
double curvature_ratio = trH * trH / detH;
if (detH < 0 || curvature_ratio > R) {
extrema.at<double>(h, w) = 0;
} else {
found++;
}
}
}
}
extremas[extrema_count++] = extrema;
}
}
cout << found;
}
int main(int argc, char *argv[])
{
namedWindow(WINDOW_NAME, WINDOW_AUTOSIZE);
int num_images = NUM_OCTAVES * NUM_SCALES;
int dog_count = NUM_OCTAVES * (NUM_SCALES - 1);
int extrema_count = dog_count - (NUM_OCTAVES * 2);
Mat src = imread(IMAGE);
Mat gray;
Mat norm;
Mat preblur;
Mat scaledUp;
Mat gauss[num_images];
Mat dogs[dog_count];
Mat extremas[dog_count - (NUM_OCTAVES * 2)];
grayscale(src, gray);
normalize(gray, norm);
gaussian_blur(norm, preblur, PRE_BLUR_SIGMA);
scale_up_2x(preblur, scaledUp);
scale_space_pyramid(scaledUp, gauss, dogs, INITIAL_SIGMA, NUM_OCTAVES, NUM_SCALES);
detect_extrema(dogs, extremas, NUM_OCTAVES, dog_count);
int i;
if (SHOW_GAUSSIANS) {
for (i = 0; i < num_images; ++i) {
imshow(WINDOW_NAME, gauss[i]);
waitKey(0);
}
}
if (SHOW_DOGS) {
for (i = 0; i < dog_count; ++i) {
imshow(WINDOW_NAME, dogs[i]);
waitKey(0);
}
}
if (SHOW_EXTREMA) {
for (i = 0; i < extrema_count; ++i) {
imshow(WINDOW_NAME, extremas[i]);
waitKey(0);
}
}
}